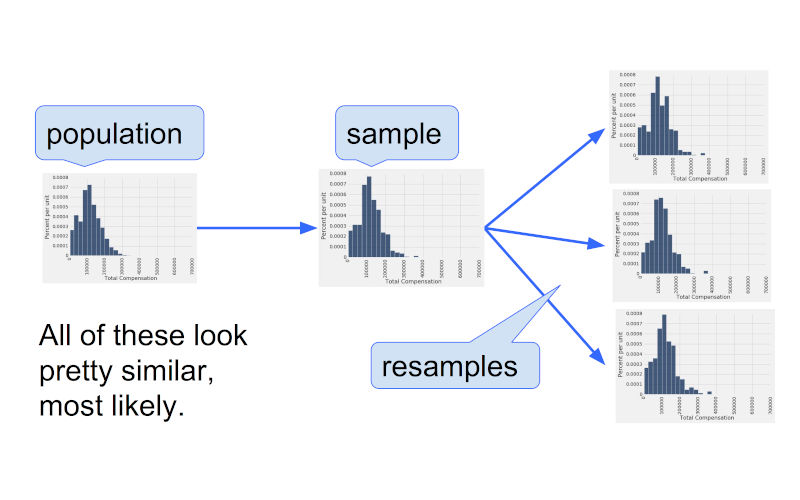
Bootstrapping in statistics is a powerful technique that allows us to estimate the properties of a statistic (like its standard error or confidence interval) by repeatedly sampling from the original dataset. It is a resampling technique used to estimate the distribution of a sample statistic by repeatedly resampling with replacement from the original dataset. This method allows statisticians to assess the variability or uncertainty of a sample statistic (like the mean, median, variance, etc.) without relying on strict assumptions about the underlying population distribution. The core idea behind bootstrapping is resampling. This involves repeatedly drawing samples with replacement from the original dataset to create multiple simulated datasets. Bootstrapping is particularly useful for estimating standard errors, constructing confidence intervals, and performing hypothesis testing. Its simplicity and effectiveness have made it a popular tool in various fields, including economics, finance, and social sciences.
Why Bootstrapping is Necessary in Statistics
Below mentioned are some reasons why bootstrapping in statistics is essential:
- Overcoming Distribution Assumptions: Traditional methods often rely on specific assumptions about the data’s distribution (e.g., normality). Whereas, bootstrapping is free of any kind of distribution, which means it works well with different data types and shapes.
- Estimating Sampling Distribution: Understanding how a statistic varies across different samples is crucial. Bootstrapping can create multiple sample datasets, thus allowing us to estimate the sampling distribution directly from the data.
- Calculating Standard Errors and Confidence Intervals: Bootstrapping provides accurate estimates of standard errors and confidence intervals without relying on parametric assumptions. This method can come handy when dealing with complex statistics or small sample sizes.
- Assessing Model Performance: It can also be used to evaluate a model’s fit and prediction accuracy. By resampling the data and refitting the model multiple times, we can assess the stability and reliability of the model.
- Handling Complex Statistics: In statistics without even knowing its theoretical properties, bootstrapping can offer a practical approach to estimate their behavior.
Also read: Data Wrangling – Understanding, Why its Important
How Does Bootstrapping Work?
- Resampling: Here we randomly select data points from the original dataset with replacement. This means a data point can be selected multiple times in a single resample.
- Creating Simulated Samples: Then we repeat the resampling process to create many simulated datasets, each having the same size as the original dataset.
- Calculating Statistics: Then the desired statistic (mean, standard deviation, etc.) for each simulated dataset is calculated.
- Estimating Properties: Finally, the distribution of the calculated statistics from the simulated samples to estimate properties of the population, such as standard errors, confidence intervals, or p-values is utilized.
Common Applications of Bootstrapping in Statistics
Bootstrapping in statistics is a versatile technique with a wide range of applications. Here are some of the most common ones:
Estimating Standard Errors and Confidence Intervals
- Complex statistics: When dealing with statistics that lack analytical solutions for standard errors (e.g., median, percentiles), bootstrapping can be a reliable estimate.
- Small sample sizes: Traditional methods at times might not be accurate with small samples, but bootstrapping can still provide with reasonable estimates.
Hypothesis Testing
- Non-parametric tests: Bootstrapping can be used to create hypothesis tests when parametric assumptions are not met.
- Complex test statistics: For intricate test statistics without known distributions, it can help determine p-values.
Model Assessment
- Model validation: Bootstrapping in statistics can be used to assess the stability and reliability of a model by resampling the data and refitting the model multiple times.
- Prediction intervals: It can help estimate prediction intervals for new data points.
Other Applications
- Outlier detection: It can also help in identification of outliers by tracking unusual data points by comparing their bootstrap distributions to the original data.
- Time series analysis: Analyzing time-dependent data by bootstrapping the residuals or creating surrogate time series.
- Survival analysis: This approach also helps in estimating survival curves and confidence intervals.
Also Read: Scorecard Model in Banking
Limitations of Bootstrapping in Statistics
Though bootstrapping in statistics is a powerful technique that allows researchers to estimate properties of a population by resampling from the original data. However, it also comes with its own set of limitations as mentioned below.
- Time-consuming: Generating thousands of resamples can be computationally expensive, especially when it comes to dealing with large datasets.
- Requires powerful hardware: Efficient bootstrapping often demands high-performance computing resources.
- Limited information: Bootstrapping can only provide information based on the data present in the original sample. It cannot uncover new information about the population.
- Sensitive to outliers: Outliers present in the original data can have significant impact on the bootstrap results.
- Accuracy depends on sample quality: Bootstrapping in statistics assumes the original sample is representative of the population. If the input sample is biased, then the results obtained via bootstrap may also be biased.
- Parametric methods might be better: When the population distribution is known or can be reasonably assumed, in those cases the parametric methods might be more efficient than the bootstrapped output.
- Specific data structures: This technique might not be optimal for certain data structures like time series data or spatial data.
- Bias in estimation: While bootstrapping in statistics can correct for some types of bias, it’s not guaranteed to eliminate all types of bias.
- Choice of bootstrap method: Different kinds of bootstrap methods can produce different results, and selecting the appropriate method can be challenging.
Addressing Limitations
- Computational efficiency: Using more efficient bootstrap algorithms or techniques like parallel processing can be considered if deemed appropriate.
- Sample size: Increase sample size to improve the representativeness of the data.
- Outliers: Identify and handle outliers appropriately before bootstrapping in statistics to avoid bias.
- Data structure: Explore specialized bootstrap methods designed for specific data types.
- Bias correction: Employing bias correction techniques in order to improve the accuracy of bootstrapped estimates.
Conclusion
In conclusion, bootstrapping offers a versatile and robust approach to statistical inference. By simulating the sampling process from the original data, it provides a practical method to estimate the sampling distribution of a statistic and construct confidence intervals. While it is essential to consider the limitations of bootstrapping in statistics, its flexibility and accuracy make it a valuable tool for researchers in various fields. As computational resources continue to grow, we can anticipate even greater advancements in bootstrapping methodology and its applications.